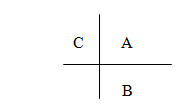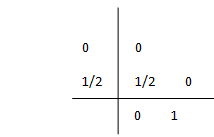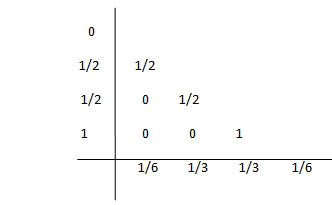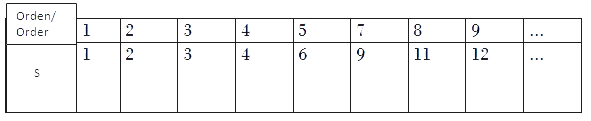Si estás buscando ejemplos o una aplicación on line sobre métodos de Runge-Kutta usa
RungeKutta Calculator.
Los métodos de Runge-Kutta son una serie de métodos numéricos para resolver ecuaciones diferenciales (o bien sistemas de ecuaciones diferenciales
Métodos lineales a un paso
Son métodos numéticos en los cuales para avanzar al paso siguiente solo es necesario la información del paso inmediatamente anterior, es decir para avanzar al paso n+1 solo es necesario la información sobre el paso n. O más formalmente
\(x_{n+1} = x_{n} + F(x_{n}, t_{n}, h) \)
\(x_{0} = x(0) \)
donde \(x_{n}\) es un vector de R
n, \(t_{n}\)>es la variable (real) independiente, h el tamaño del paso, y F es una función vectorial de x
n, t
n, h, es decir
\( F: \mathbb{R} ^{n+2}\mapsto \mathbb{R} \)
Obsérvar que este es en realidad un sistema de ecuaciones.
Hay otros métodos llamados multipaso, en los que pasa avanzar al paso siguiente son necesarios dos o más pasos anteriores, no los trataremos aquí. También hay otros métodos no lineales, tampoco los discutiremos aquí
Los métodos de Runge-Kutta methods son un caso particular o una especialización de los métodos numéricos a un paso.
Lo que caracteriza a un método de Runge-Kutta es que el error tiene la forma
$$E_{i}=Ch^{k}$$
Donde C es una constante real positiva, el número k es llamado
orden del método
El número de etapas del método Runge-Kutta es el número de veces que se evalúa la función en cada paso i, este concepto es importante porque la evaluación de la función requiere un costo computacional por eso, son preferidos métodos con un número tan mínimo de etapas como sea posible.
Ejemplos de métodos de Runge- Kutta
El método de Eule (Runge-Kutta de orden 1)
$$x_{n+1} = x_{n} + h f(x_{n}, t_{n}) $$
El error es en forma de \(e \le = Ch\), por eso este método tiene orden 1
Nota: La función se evalua una vez en cada paso, por eso el número de etapas es 1.
Regla del punto médio (Runge-Kutta de orden 2)
$$x_{n+1} = x_{n} + h f(x_{n}, + \frac{h}{2}f(x_{n},t_{n}),\, t_{n}+\frac{h}{2}) $$
El error es ahora en forma \(e \le = Ch^{2}\) por eso este método tiene orden 2
Nota: La función se evalua dos veces en cada paso, por eso el número de etapas es 2.
Runge kutta estandar de orden 4(Runge-Kutta de orden 4)
$$x_{n+1} = x_{n} + \frac{h}{6}(k_{1} + 2k_{2} + 2k_{3} + k_{4})$$
donde
\( k_{1} = f(x_{n}, t_{n})\)
\( k_{2} = f(x_{n} + \frac{h}{2} k_{1}, t_{n} + \frac{h}{2})\)
\( k_{3} = f(x_{n} + \frac{h}{2} k_{2}, t_{n} + \frac{h}{2})\)
\( k_{4} = f(x_{n} + h k_{3}, t_{n} + h)\)
El error es ahora en forma \(e \le = Ch^{4}\) por eso este método tiene orden 4
Número de etapas: 4.
Gráfica del error/h
|
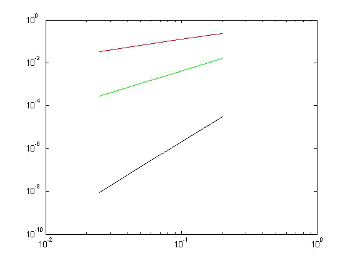 |
gráfico del Error/tamaño de paso
en escala logarítmicade los tres métodos vistos aquí:
- Euler
- en verde la regla del punto medio de orden 2
- En negro Runge-Kutta clásico
Notar como la pendiente se incrementa con el orden del método. |
Adoptamos la siguiente definición de un método de Runge-Kutta
Método de Runge-Kutta
Un método de Runge-Kutta con s etapas y orden p es un método numérico de la forma
\( x_{n+1} = x_{n} + h \sum_{i=1}^{s}b_{i}k_{i} \)
Con
\( k_{i}= f(x_{n} + \sum_{j=1}^{s}a_{ij}k_{j}, t_{n}+hc_{i}) \)
Y el error verifica la condición
\(Max|x(t_{i})-x_{i}| \le Cht^{p}\)
Así para dar un método de Runge-Kutta es necesario dar los s
2 + 2s números, que son
$$b_{i}, c_{i}, a_{ij}$$
Una característica interesante de los métodos de Runge-Kutta es que no es necesario calcular derivadas de f para avanzar. El precio a pagar es evaluzar más veces la función con el consiguiente coste computacional.
Convergencia de los métodos de Runge-Kutta
Sea F una función
Lipschitz en x
Entonces
$$ Max|x(t_{i})-x_{i}| \le \frac{K(e^{Lb} -1)}{L} $$
donde L es la
constante de Lipschitz de F y K es el error de truncación local.
En método es más eficiente que otro si tiene un número reducido más de etapas, manteniendo el orden. Por ejemplo, entre un método de 3 etapas
con orden 3 y otro con 4 etapas y orden 3, es mucho más interesante el primero de ellos con la misma longitud de paso ya que número de cálculos será
menor para él.
Tableros de Butcher
Dado un método de Runge-Kutta, construimos un tablero como sigue

También es posible escribir como tablero de Butcher
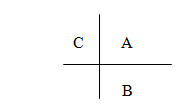
Donde A ∈ M
sxs, b ∈ R
s, C ∈ R
s
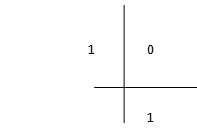
Por ejemplo, el talero de Butcher para el método de Euler es
Para el punto médio de orden 2
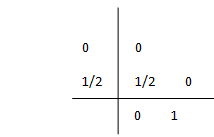
Y para el Runge-Kutta estandar de orden 4
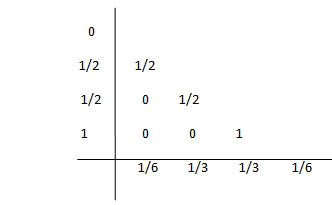
Un método de Runge-Kutta, se dice que es consistente si el error de truncación global tiende a cero cuando el tamaño de paso tiende a cero.
Se puede demostrar que una condición necesaria y suficiente para la consistencia de un método de Runge-Kutta es que la suma de los b
i sea igual a 1
es decir si se satisface que
$$1=\sum_{i=1}^{s}b_{i}$$
Además el método es de orden 2 si se cumple que
$$ 1= 2\sum_{j=1}\sum_{i=1}^{s}a_{i}b_{j} $$
Condiciones parecidas se pueden dar para métodos de orden 3, 4, etc.
Métodos de Runge-Kutta explícitos
En un método de Runge-Kutta explícito, en la definición de los k
i no aparece como función de ellos mismos, es decir
, la matriz del tablero de Butcher del método es "casi triangular inferior", porque es triangular inferior excepto por los elementos en la diagonal, los cuales también son cero

Teorema
Un método de Runge-Kutta explícito con s etapas no puede tener orden mayor que s.
Se sabe que no hay métodos de Runge-Kutta explícitos con s etapas con orden s para s mayor o igual que 5.
También se sabe que no hay métodos de Runge-Kutta explícitos con s etapas con orden s-1 para s mayor o igual que 7
Con más generalidad, tenemos la siguiente tabla
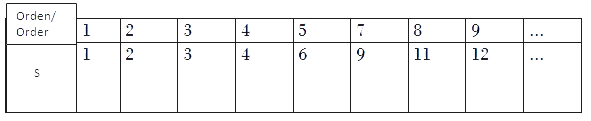
¿Que tamaño de paso es necesario? La respuesta depende del problema específico, el grado de precisión requerido y el costo en tiempo que pretendemos gastar.
Otra cosa importante a considerar en los métodos de Runge-Kutta es que hay cierta pérdida de precisión cuando la derivada de la función es grande
o bien cuando cambia frecuentemente de signo, tales casos requieren tomar un tamño de paso menor para obtener el grado de precisión requerido.
En la siguiente sección veremos los
pares encajados de Fehlberg
, que son métodos en los cuales el tamaño del paso se ajusta automáticamente dependiendo (entre otras cosas) de los cambios en la derivada de la función
Para ver un ejemplo de como trabajan estos métodos, consulta
RungeKutta Calculator
donde verás el problema por defecto
$$ \left\{\begin{matrix} y'=f(x,y) & \\ y(x_{0})=y_{0} \end{matrix}\right. $$
Cuya solución exacta es obvia \(y=e^{x}\).